Тайны квадрата Пифагора
«В начале было Число, и Число было у Бога, и Число было Бог»
HOMO LUDENS
Таблицы Пифагора (и многозначные числа)
Число постоянно переосмысливалось и изучалось человеком. С помощью числа человек познавал мир. Порою казалось, что человек играет с числом, а иногда, – что число играет человеком. Человек привыкает к числу и вот иже он становится от него зависим, он не может жить без него. В любом предмете, в любом явлении он видит числовые структуры, язык чисел. Игра и число всегда шли рядом. Игра была спутником человечества с незапамятных времен. Мир игры это, кроме всего прочего, своеобразный грандиозный музей истории культуры... В игре, как и в иных культурных явлениях, своеобразно отражаются конкретные условия развития того или иного общества, этапы его истории[1]. Скажу больше, именно игра – первооснова искусства. Музыка, песня, танец – это ведь и есть игра. Обычно игра воспринимается как нечто несерьезное и шутливое и крайне противоположное работ (физическому труду). Задумывались ли вы над тем, что скрывается за понятием «игра», почему человек играет? В первую очередь игру следует воспринимать как восприятие человеком сложных мировых процессов. Именно игра создает правила и упорядочивает сложные процессы. Сама жизнь воспринимается как игра. Иногда игра может увести слишком далеко от реальности и тогда человек не может существовать вне игры, следуя ее правилам человек создает замкнутый мир иллюзий и несбыточных желаний. Человек заигрался и азарт может погубить его в расцвете сил. (Вспомним пословицы «игра до хорошего не доведет», «важно вовремя выйти из игры»...) Искусство – это игра. Это искусственный мир, который строит человек в противовес природе. Игра побуждает спор. Весь хваленый прогресс (НТП и НТР) есть не что иное, как замена живого искусственным. (Кажется, что человек тщится повторить действия Бога, который играя однажды вылепил из глины людей.) Даже себя человек пытается заменить роботами.
Игра не есть атрибут лишь человечества. В игры играют и звери и насекомые, но они, по-видимому, не осознают числа и пропорций, а лишь интуитивно чувствуют их. Игры изначально несли сакральный характер с долей эротизма (посвящения, любовные игры). Поэтому игры порою неотличимы от обрядов и ритуалов.
|
Шахматная доска |
Непредсказуемость ситуации люди пытались разрешить игрой с жесткими правилами, надлежащим увеселением, вызываемым декорациями. Игра тесно связана с гаданием, а вместе с ним и с определенной философской системой. Игра улаживала спор между соперниками и давала однозначные ответы «да» или «нет» на поставленные вопросы. «И-цзин», «каббала», «таро» – наиболее известные гадательные и философские системы со временем становятся всего лишь примитивными играми. В старину, например, не только играли в шахматы и домино, но и гадали на них. «В древних литературах то и дело встречаются легенды о мудрых и магических играх, которые были в ходу у монахов, ученых и при гостеприимных княжеских дворах, где фигуры и поля имели, кроме обычных, еще и тайные значения». (Г. Гессе «Игра в бисер»). Каждая игра (будь то шахматы, шашки, го, домино...) – это иерархия божеств, структура мироздания. Самая известная игра интеллектуалов, – несомненно, шахматы. Шахматы не являются чисто индийским изобретением. У каждого развитого народа существовала подобная игра. Индийцы просто смогли великолепным образом представить эту игру миру, снабдив ее туманным философским смыслом. Шахматы отражают борьбу черного и белого. Само поле битвы (шахматная доска) перемежается черными и белыми квадратами. Таких квадратов 64; 8х8). Поле битвы разделено на две части. Водной части стоит черное войско, в другой – белое. В древние времена игре придавали огромное значение, ибо игра связана с судьбой. Отсюда такая любовь древних к жребию. Важно отметить, что понятие мирового периода (юги) было заимствовано индусами из игры в кости.
На Руси была известна игра в бирюльки – маленькие поделки в виде бочонков, корзинок, колечек, которые складывались в кучу. Нужно было крючком вытащить одну из них, не затронув остальных. Известно было также гадание на бобах. «Цибела старая во многих там избах Загадывала всем о счастье на бобах» (В. Майков «Елисей или раздраженный Вакх»). Русская игра в городки отразилась в понятии «бить баклуши», т.е. пустое времяпрепровождение (баклуши – деревянные чурки) И из игры в бирюльки, и из игры в городки можно выстроить философскую систему типа таро или И-Цзин, если такая философия не есть изначальное условие всякой игры. Немецкий философ Г. Гессе посвятил игре целую книгу, где есть такие строчки:
Игра нам в радость. Нас не гонит плеть
В пустыне духа не бывает гроз
Но в тайне мы мечтаем жить всерьез,
Зачать, родить, страдать и умереть...
...Он сидит на пепелище. Бусины в руке,
Когда-то шифр науки многомудрой,
А ныне просто стеклышки цветные,
Они из дряхлых рук скользят бесшумно
На землю и теряются в песке...
Обратимся теперь ко всем известной «Таблице умножения» Пифагора. Здесь числа приведены к определенной системе и разнесены по графам. Таблица имеет столбцы (вертикальные строчки) и колонки (горизонтальные строчки). Считается, что таблица Пифагора служит лишь для удобства счета, однако достаточно знать кое-что о философской системе Пифагора, чтобы в этом усомниться. Пифагор придавал числам мистические свойства, считал, что числа правят миром. Из этого можно вывести, что и саму таблицу умножения этот философ считал отображением вселенной, где угадывается за закономерностью чисел ровный строй планет и скоплений звезд, где угадывается гармония космоса и слышится божественная музыка.
Каждый уважающий себя школьник, которому гранит науки стал поперек горла, лютой ненавистью ненавидит Пифагора с его злосчастной таблицей умножения и прочими премудростями... Между тем, одна эпоха сменяет другую, а таблица Пифагора все также смотрит на нас с обложки тетрадки в клеточку.
Но в том виде, к какому мы привыкли, таблица Пифагора появилась лишь в VI в., когда в Европе появились арабские цифры. До этого греки пользовались вместо чисел буквами алфавита. Итак, загадка первая — для чего нужна была древним грекам таблица Пифагора? Без десятичной позиционной системы счисления от нее мало толку. Есть предположение, что она поначалу была наглядным примером пропорциональности чисел. Ведь Пифагор считал, что сущность красоты кроется в соотношениях между цифрами.
Рисунок 1 |
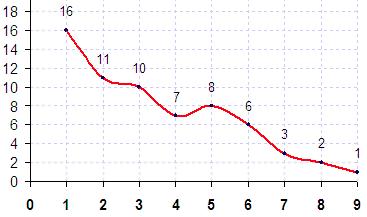 |
А теперь ближе к делу. Однажды как-то решил заменить двузначные числа таблицы Пифагора разностью их цифр (давайте договоримся, что многозначные числа состоят из цифр) – 18 – это 7, а 27 – это 5 и т.д. Если каждому числу присвоить какой-либо цвет и раскрасить таблицу, то вырисуется стройная картина из трех концентрических кругов (см. рис. 1). В самом центре таблицы – скопление четырех чисел, дающих в разности «3». Круг поболее, из восьми чисел, объединяет их по разности «2». И наконец, третье кольцо составлено из 16-и чисел (вычитание двух цифр здесь составляет «1»).
Рисунок 2 Порождение «»числовой материи Пифагора из «числового вакуума» |
|
|
|
|
|
Нетрудно заметить, что такая преобразованная таблица Пифагора обладает симметрией. Одни и те же числа встречаются в ней часто, но распределены по всей площади по какому-то своему закону. Больше всего встречается единиц-, а вот меньше всего девяток (вместе с тем семерок меньше, чем восьмерок.
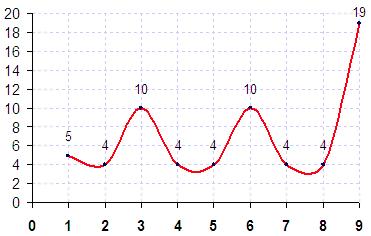
На рис. 2 изображено, что будет с таблицей Пифагора, если многозначные числа складывать до однозначных. Например, 18 – это 9 (1+8), 56 – это 2 (5+6=11, 1+1) и т.д. Видно, что в этом случае вырисуется ось симметрии, а внутри самой таблице еще одна маленькая табличка.
Рисунок
3 |
 |
Еще одно замечательное свойство такой таблицы (см. рис. 3). Если поочередно вычитать соседние цифры (сначала в строках, а затем в столбцах), то в конечном итоге получится ноль, как ни крути. Может быть, это служит еще одним подтверждением пифагорейского учения о возникновении «числовой материи» из вселенского вакуума, из пустоты. Мысль Пифагора о том, что все. можно вывести из единицы и все можно к ней же и свести, перекликается со словами из Библии: «Ибо прах ты, и в прах возвратишься...»
Считается, что таблица Пифагора служит только лишь для удобства счета, однако, как мы это уже увидели, достаточно знать философский настрой «первого в мире статиста», чтобы в этом усомниться. Вполне возможно, что свою таблицу Пифагор считал отображением устройства космоса (это слово, кстати, придумано Пифагором, равно как и понятие «философия»). Закономерность чисел – это ровный строй планет и хаотическое скопление звездной пыли – и во всем этом слышится музыка сфер... К слову, великий Кеплер на полном серьезе считал, что Сатурн и Юпитер поют басом, Марс – тенором, Земля и Венера – альтом, а Меркурий – дискантом. Вспомним, с каким едким сарказмом поносили пифагорейскую мистику чисел философы-прогрессисты. Прошло время, и о Пифагоре вспомнили физики, столкнувшись со строго фиксированным набором фундаментальных констант. Да и в наш компьютерный век мы воспринимаем мир преимущественно через число. Большое распространение получила цифровая запись информации, когда речь, музыка и текст преобразуются в числовой код и фиксируются в виде электросигналов...
А что Пифагор? Он, как современник Конфуция, Будды и Заратустры, воспринимался в греческом мире не только ученым, но и пророком. Он, как Иисус, говорят, ходил по воде, предсказал рыбакам их богатый улов и принял мученическую смерть. Некоторые считали его «последним человеком с Атлантиды», а один итальянский историк назвал как-то Пифагора «античным фашистом». Рассказывают даже, что Пифагор укусил ядовитую змею, которая попалась ему на пути и поплатилась своей смертью за неуважение к математике. Что ж, будем почтительны к его наследию и мы, иначе рискуем на себе испытать острые зубы какого-нибудь местного неопифагорейца. Как говорил В. Хлебников, «Природа чисел та, что там, где есть «да» числа и «нет» числа (положительные и отрицательные существа), там есть и мнимые (√-1)».
Для анализа таблицы Пифагора сведем двузначные числа к однозначным путем разности двух цифр (48=8−4=4; 36=6−3=3...). Для наглядности присвоим каждому однозначному числу цветовое обозначение.
Из рисунка видно, что структура таблицы имеет кольцевой характер. Отчетливо видны три концентрических кольца, сформированных вокруг единого центра. Размеры трех колец (условно обозначенных как «черное», «красное» и «оранжевое») соотносятся как 4:8:16 или 1:2:4. (Сравните пропорции трех колец в гл. «Структурология каббалы»).
«Таблица» состоит из четырех частей, на которые ее делят две оси: горизонтальная и вертикальная. Существует еще ось симметрии, поэтому верхний левый квадрант таблицы несколько отличен от трех других. «Черное кольцо» составляют числа, дающие в разности единицу, т.е. их цифры наиболее удалены друг от друга (слабое взаимодействие). «Красное кольцо» состоит из чисел, которые дают в разности «2». Оранжевое кольцо наиболее стянуто. Опираясь на таблицу Пифагора можно построить три кольца в соотношении 4:8:16 (или 1:2:4) Толщину каждого кольца вычислим путем суммы цифр числа, входящего в какое-либо кольцо. (Толщина будет переменной). Например «оранжевое кольцо» (размер = 4). Толщина 25=7; 30=3; 36=9.
Разность выделила из таблицы три окружности.
Сумма придала им телесность (толщину).
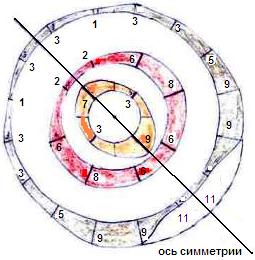
Количественное содержание колец:
| 1: | 2: | 3 |
| 4: | 8: | 16 |
Несомненно, что числа, заполняющие таблицу Пифагора выявляют асимметрию (неравномерность) пространства. Задолго до Эйнштейна Пифагор размышлял над искривлением и неоднородностью космоса. По Пифагору пространство можно описать девятью числами не считая нуля (при десятеричном исчислении). Другими словами пространство насчитывает девять структурологических видов. Причем 9,8,7,6 структуры пространства являются главными (наиболее полными), остальные структуры являются лишь повторением главных. Структура же числа «1» вообще является простейшей и может даже не рассматриваться. В таблице Пифагора наиболее важной частью является верхний правый квадрант. Особо остановимся на девятом структурологическом виде пространства (СВП). Не трудно заметить, что числа в девятом столбце таблицы Пифагора ведет себя странно. Так, например, числу 18 соответствует число «81». Причем числа 18 и 81 максимально разнесены (удалены друг от друга). Или, например, числу 45 соответствует 54 (причем они стоят рядом). Таким образом девятый СВП зиждется на оборотных числах. Подмечена также интересная закономерность оборотных чисел:
871−178=7∙9=770−7=92−29=693
18Σ=27Σ=36Σ=...9
Поэтому умножение любого числа на 9 можно заменить вычитанием. Например, 19374∙9=193740−19374=174366
Числа других СВП ведет себя несколько иначе, хотя для всех СВП верно выражение, несколько приоткрывающее смысл вышеуказанных закономерностей
[aa0]−(10−x)∙a=a∙x для чисел типа 10, 20, 30...90
aa0−0aa=a∙9 т.е 90−09=9∙9
aa0−a∙2=a∙8 т.е 20−2∙2=2∙8
aa0−a∙3=a∙7 т.е 20−2∙3=2∙7
Если просуммировать цифры чисел таблицы умножения Пифагора, то получится таблица суммы. Она кажется менее интересной, чем таблица разности. Хотя следует отметить странное образование квадрата внутри таблицы и вместе с этим эксцентриситенное смещение точки пересечения осей (центра). Кроме этого обращает на себя внимание весьма равномерное распределение «чисел суммы» (Σ) по объему таблицы. Хотя за исключением числа девяти (Σ=9), образующего так называемый гномон вырисовывающихся фигур не наблюдается.
Более или менее равномерное распределение чисел (Σ) выглядит рассеянным. Разность соединяет, сумма разъединяет. На примере таблицы Пифагора можно доказать еще один постулат: Все можно свести к единице и все можно вывести из единицы. Представим известную уже таблицу «Разности».
По горизонтали сгруппируем числа по два и вычтем одно из другого (т. о. Таблица в два раза сократится в ширину
Затем сгруппируем полученные числа по вертикали и вычтем друг из друга. Т.о. таблица сократится в 4 раза
Вновь сгруппируем числа по горизонтали и вычтем одно из другого
И так до тех пор, пока не получим квадрат из четырех единиц.
Эти единицы взаимоуничтожаются, превращаясь в ноль. Этот наглядный пример творения из ничего. Как сказано в Библии «Ибо прах ты и в прах возвратишься». Весь мир со своим безумством красок предстает мыльным пузырем. (Некоторая аналогия с теорией раздувающейся вселенной). Человек ли, земля наша - не есть ли мыльный пузырь, который кажется огромным и невесомым? Но вот лопается его радужная оболочка и от былого величия не остается и следа. Ноль – это по сути вакуум (активная среда непрерывно рождающихся и исчезающих элементарных частиц).
Не меньший интерес, чем таблица умножения представляет таблица степеней, где рассматриваются числа типа am. Главная особенность «таблицы степеней» - это то, что здесь является важным неравенство am≠ma (не считая некоторых исключений типа 22=22 или 23≈32).
| am | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 |
|
8 |
16 |
32 |
64 |
128 |
259 |
512 |
| 3 |
9 |
27 |
81 |
243 |
729 |
2187 |
6561 |
19683 |
| 4 |
16 |
64 |
256 |
1024 |
4096 |
16384 |
65536 |
262144 |
| 5 |
25 |
125 |
638 |
3190 |
15950 |
79750 |
398750 |
1993750 |
| 6 |
36 |
216 |
1296 |
7776 |
46656 |
279936 |
1679616 |
10077696 |
| 7 |
42 |
294 |
2058 |
14406 |
100842 |
705894 |
4941258 |
34588806 |
| 8 |
64 |
512 |
4096 |
32768 |
262144 |
2097152 |
16777216 |
134217728 |
| 9 |
81 |
729 |
6561 |
59049 |
531441 |
4782969 |
43046721 |
387420489 |
Многозначные числа сведем к однозначным, просуммировав их цифры (т.е. составим «таблицу суммы»)
Рисунок 1 |
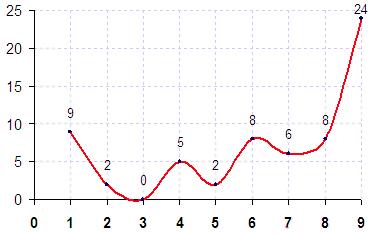 |
На таблице вырисовываются горизонтальные линии, состоящие из «9» и «6». Остальные колонки (строчки) таблицы предстают как периодические зависимости. Чем выше строка таблицы, тем более длительны эти периоды. Числа как бы переходят от меньшей упорядоченности к большей. И такое движение происходит сверху вниз. Крайне любопытно, что однородные периоды имеют не только числа, кратные трем, но и число семь:
[(3n)m]Σ = 9.
(7m)Σ = 9
Также обращает на себя внимание не менее интересный феномен - отсутствие в таблице числа три:
[(3n)m]Σ ≠ 3. Это явление наблюдалось экспериментально от 1 до 9, но можно предположить, что такая закономерность сохраняется и для чисел более высокого порядка.
Аналогичная таблица Пифагора в китайской гадательной традиции существует таблица гексаграмм.
Из нее видно, что гексаграммой (шестью чертами) можно выразить любое число от 0 до 63 (всего 64 числа). Именно 64 гексаграмм содержит китайская «Книга перемен» (И-цзин). Именно 64 клетки на шахматной доске. Именно 64 числа в таблице Пифагора. Число «8» очевидно наилучшим образом подходит для размера любых таблиц, служащих не только для счета, но и для философского подхода к этому миру.
Пифагор не был одинок в своем стремлении соотнести число с определенной структурой. В XVII в. французский математик, физик и философ Блез Паскаль разработал арифметический треугольник чисел, названный его именем. Наращивание треугольника Паскаля связано с единственной операцией – сложением.
Если строкам присвоить индекс n, а столбцам – k, то можно вычислить биноминальный коэффициент:
1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
«Треугольник Паскаля таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных численных схем во всей математике». (М. Гарднер).
Перевернем треугольник таким образом, чтобы получилась таблица Паскаль рано попал под влияниерелигиозного учения янсенизма и ушел в монастырь. Его философское сочинение «Мысли» выражают разочарование в силе разума и апологию христианства.
КСТАТИ
Природа числа с течением времени постоянно уточняется. Пропорции явили миру дробные (рациональные) числа. Решение задачи на вычисление сторон треугольника привело к появлению иррациональных чисел. А вычисление квадратных и кубических уравнений не может обойтись без мнимых чисел, открытых лишь в XVI в. Свойства целых чисел изучаются в специальном разделе математики—теории чисел. Пожалуй, только она может объяснить, почему разность зеркальных чисел (81-18,73-37 и т. д.) всегда кратна девяти, почему при умножении на 5 получается число с пятеркой или с нулем на конце, почему деление на 9 часто дает периодическую дробь. А как вам такой пассаж? Любое число, возведенное в третью, шестую или девятую степень, дает число, последовательная сумма цифр которого всегда получается равной девяти. Можете проверить, если не верите.
[1] Ю.В. Бромлей, Р.Г. Подольный «Создано человечеством»
И.В. Карасев, 1997
См. также:
Поголовный отсчет. Является ли
многоголовость, многорукость, карликовость и гигантизм мифических героев
следствием высокого развития индоевропейской науки счисления?
Самые необычные системы
считсления
Мантические
числа Книги Перемен
Нумерология. Начало прогнозиса
ПРОГНОЗЫ:
Крадущийся тигр, затаившийся закон (2010) | Одолеют ли быки медведей (2009) | Кракатук, или мышиный король (2008) | Золотая свинья на свинцовых ногах (2007) | Собачьи бега (2006) | Петушиные бои (2005) | Обезьяньи хлопоты (2004)
|
|